- LEAST KINO : Baby's first classical mechanics and any kind of simple applied mathematics where the mathematics is just being perverted and used to an end. Chemistry and biology are often guilty of this too. Dear chuds, mathematics is an end in itself, I'm gatekeeping it from you.
- Applied mathematics where the mathematics itself ends up being interesting in its own right. Examples: Statistics, Partial Differential Equations arising from physical models, Game Theory used for economics, Quantum Group Theory and manifolds in General Relativity.
- Applied mathematics in the sense of computer science e.g. computational complexity classes. This leans on the abstract and hence you are far more free to stop caring so much about the real world and explore the wonderful language game, Mathematics, whose rules are spookily enforced by the universe.
- "Useful" pure mathematics such as analysis. I admit I actually love analysis, but it's not kino for the simple reason it's too useful for humanity, and humanity is vile. Mathematics has no need for the flesh.
- Geometry. It's too useful to be given a high ranking. Also, it's not really very interesting to modern mathematicians except when viewed through the lense of algebra or topology.
- Rigorous analysis and integration with Measure Theory, tied with Number Theory. Both filter out casuals because they aren't obviously useful, though you do get a lot of people who think they can give a short proof of Fermat's Last Theorem with zero formal training to this day. Ranking isn't that high because both end up being kind of messy, Number Theory and Additive Combinatorics especially start getting really deranged with their inequalities and Landau notation for bounds.
- Linear algebra. It's actually very fun, people seem to have bad experiences with it and find it boring (even a lecturer of mine). It's not, but I do admit it's very 'clean', you aren't in for many weird surprises. The reason physicists love it so much is precisely that you get a lot of orderly stuff going on.
- Group Theory, Ring Theory, Algebras, Modules. This is basically where the fledgling kino of Linear Algebra blossoms into true unadulterated uselessness and surprising theorems, and as you should understand by now, uselessness is an almost exact measure of how kino a field of mathematics is.
- Weirder kinds of algebraic structures. Graph Theory, Monoids, Topologies, Category Theory, Galois Theory. The study of geometry in a more formal setting with respect to algebraic equations is here too I would imagine, but I don't actually have much background in this so I can't confirm. All of these things threaten to become so abstract that normies have an immediate gag reflex, physicists start crossing themselves and throwing salt over their shoulders to ward off curses.
- The last possibly applied topic is here, actually: Formal Logic. I don't count this as useful however, as not only is it so divorced from any mathematics you've seen at school it will cause a panic attack in the vast majority of applied-brains, but analytic philosophers are the only people who actually find it useful, along with some computer scientists. And analytic philosophy in some senses predates mathematics, so one could even say that this kind of mathematical study of logic is applied philosophy. Stuff like Lambda calculus, first order logic, deviant logics etc. go here.
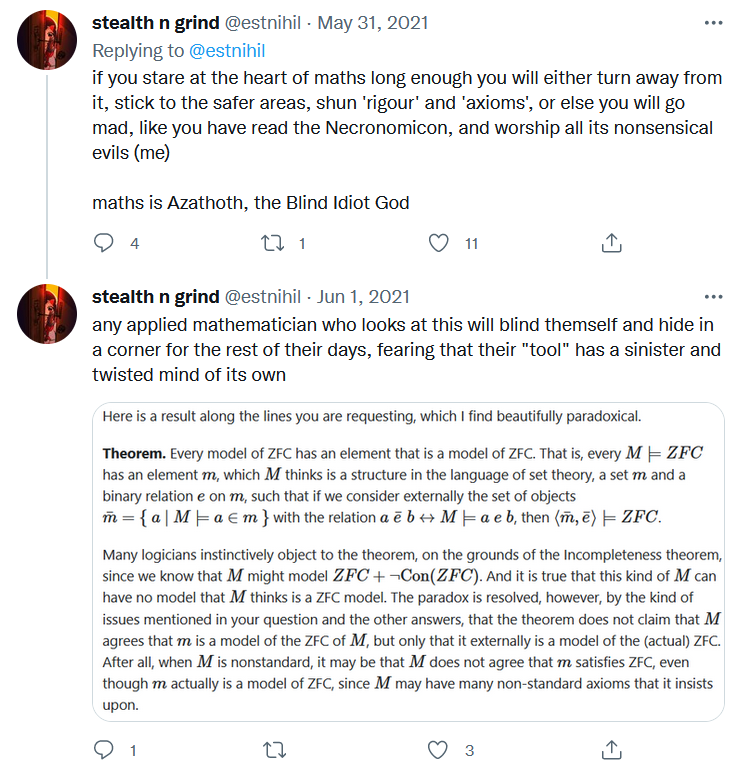
- TOP TIER KINO: Metamathematics . This is the holy grail of utterly useless yet DIVINE and far-reaching mathematics. None of the results make intuitive sense. Godel's Incompleteness Theorems provide a sense of lingering cosmic horror and 'results' can be highly sensitive to the axiomatic system you're working with. You can try to provide a use case to someone by saying, "Well if we show the truth status of this conjecture is independent of ZFC, then we could simply take the truth of it as an axiom" and they will simply cry. It's genuinely frightening that mathematics can talk about itself and in such a way that makes physicists permanently seethe, and that's why it's the most kino kind of maths.